How discriminator losses and normalization can be used to transfer semantic content and style information. A summary of work by Buhler et al, 2019.

The following is a snippet from my first doctoral exam.

Background

A particular challenge in gaze prediction is a lack of data to apply sophisticated models that may be better able to model eye behavior. In fact, lack of high quality eye tracking data is a problem in the field of HCI ¹², presented by individual variability, privacy concerns and noise in signals from sensors that may be more ubiquitious (e.g., laptop cameras) but imprecise compared to more reliable, in-lab setups (e.g., with IR sensors). Buhler et al³ address this problem through an application of GANs capable of generating data that maintain both the semantic and style information contained in images of the eye. The authors aim to generate eye image data that preserves the semantic segmentation of eye features (i.e. pupil, iris, sclera) relevant to gaze prediction while also modeling participant-specific eye style, characterized by perceptual features such as skin quality around the eye or sclera vasculature.

The main problem the authors address is the lack of 2D eye images, collected from infrared cameras sensors, for model training. Specifically, they sought to improve data volume for training gaze estimation models under occlusion in VR, synthesize person-specific eye images that satisfy a segmentation mask and follow the style of a specified person from only a few reference images. Furthermore, the authors propose a method to inject style and content information at scale, which has implications past HCI to clinical diagnoses using eye behavior markers in patients with scleritis, autism or schizophrenia ⁴⁵⁶.

The authors modify GANs, adversarial networks which typically take random noise as input. By introducing noise, the model can produce data from a variety of locations in the target distribution, subsequently transforming the noise into a meaningful output. In implementation, GANs utilize two loss functions: one that is designed to replicate a probability distribution through generation of new image instances, hence "generative," and another that acts as a discriminator which outputs a probability of the new image instances being real. Because the authors work relies on extensive technical background, the focus of this brief will cover the design of discriminator loss functions to quantify segmentation and style difference between "fake" and "real" images and the use of normalization to generate convincing fake images. These are critical to understanding recent and future applications of GANs to clinical image data, specifically in the generation of artificial eye images through the authors' proposed Seg2Eye network.

Preserving eye image style through losses and normalization

First we define the simple way in which style information difference is quantified across two images by the discriminator. The output of a kernel (i.e., filter) applied to a convolutional layer (\(l\)) forms the feature map (\(F^l\)) associated with the layer. The Gram matrix ⁷ is computed using data from specific layers and on a number of feature maps (\(N_l\)). It is a quantification of the similarity between features in a layer, across all feature maps. The \(N^l \times N^l\) Gram matrix is composed of elements indexed by maps \(i, j\):

\[ \mathbf{G}^{l}=\left\langle\mathbf{F}_{i:}^{l}, \mathbf{F}_{j:}^{l}\right\rangle = \left[\begin{array}{c} \mathbf{F}_{1:}^{T} \\ \mathbf{F}_{2:}^{l}{ }^{T} \\ \vdots \\ \mathbf{F}_{N_{l}:}^{l} \end{array}\right]\left[\begin{array}{llll} \mathbf{F}_{1:}^{l} & \mathbf{F}_{2:}^{l} & \cdots & \mathbf{F}_{N_{l}}^{l} \end{array}\right] \]

where \(\mathbf{F}_{i:}\) represents the column representation of a feature map \(i\). The Gram matrix has been effectively used to quantify the amount of style loss of a generated image \(\hat{I}\) with respect to a style target image \(I\). The style-specific loss \(\mathcal{L}_{\text {Gram}}\) is calculated by Buhler et al as:

\[ \mathcal{L}_{\text{Gram}}=\Sigma_{i=2}^{m}\left\|\mathbf{G}^{l}\left(F_{E}(\hat{I})\right)-\mathbf{G}^{l}\left(F_{E}(I)\right)\right\|_{1} \]

where \(E\) is a style encoder trained to discriminate between feature map activations of (real) style images and m is the number of feature maps in \(E\). The style loss metric computes the L1 distance (i.e. sum of absolute differences) between a generated and target image feature maps at the Seg2Eye discriminator layer \(l\). Thus, the style encoder is trained to distinguish between feature map activations of different styles of eye images, and this information is used in place of calculating the Gram matrix from feature maps within the Seg2Eye network downstream.

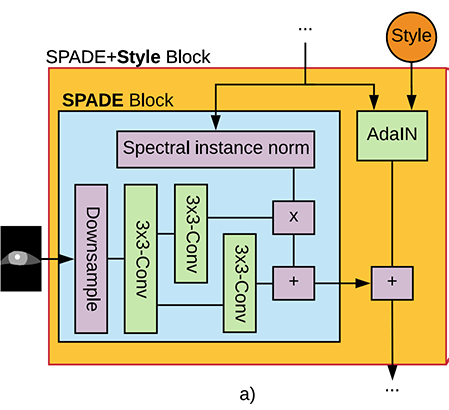
Another key aspect of Seg2Eye is the use of adaptive instance normalization (AdaIN) by the generator, which replaces batch normalization typically used in deep networks for the purposes of style transfer. While batch normalization has arguably been one of the core advancements that has made deep learning feasible for a wide range of biomedical problems ⁸, normalizing batches of data loses style information. AdaIN uses style input to align the channel-wise mean and variance of a content input to match the style. In Seg2Eye, this is used after a convolutional network layer to normalize the generated image statistics using the style reference from a human's eye (Fig. 2a in ⁹), transferring qualities such as sclera perforations and skin around the eye to the generated image. For a given style reference image, AdaIN uses its layer activations \(r\) and computes its mean \(\mu\) and variance \(\sigma\) from a layer:

\[ \mu_{n c}(r)=\frac{1}{H W} \sum_{h=1}^{H} \sum_{w=1}^{W} r_{n c h w} \\ \sigma_{n c}(r)=\sqrt{\frac{1}{H W} \sum_{h=1}^{H} \sum_{w=1}^{W}\left(r_{n c h w}-\mu_{n c}(x)\right)^{2}+\epsilon} \]

where \(H, W\) represent the dimensions of the activations and \(n, c\) represent the batch and channel (i.e. layer) respectively. Then, for a generated image, the AdaIN block uses the \(\mu(r)\) and \(\sigma(r)\) when scaling activations during learning:

\[ \operatorname{AdaIN}(x, r)=\sigma(r)\left(\frac{x_{nc}-\mu(x)}{\sigma(x)}\right)+\mu(r) \]

where \(x\) refers to the normalized image activations associated with the generated image. AdaIN allows each sample to be normalized distinctly (unlike batch normalization), and furthermore utilizes first- and second-order statistics of preferred activations from the reference style image. Through shifting and scaling layer activations of the generated image via AdaIN and minimizing a loss function (\(\mathcal{L}_{\text {Gram}}\)) which compares feature maps between the generated and reference image, the network maintains the content's spatial information but uses the human eye reference image to infer style information critical to preserving perceptual similarity of the eye. This was an important goal for the authors to improve data generation methods.

Preserving eye image segmentations through losses and normalization

A notable aspect of Seg2Eye is its input: rather than random noise typical of GANs, it utilizes more contextual information in the form of a segmentation mask. In this case, the reference image of the map consisted of a pupil, sclera and iris segmentations. While the Gram matrix is useful for quantifying the difference in consistency of feature maps across images by the discriminator, simply taking the distance between feature maps allows us to learn broad content information contained in an image through a previously proposed ¹⁰ loss function:

\[ \mathcal{L}_{\text{\mathcal{D}_F}}=\Sigma_{i=2}^{m}\left\|F_{D}^{l}(\hat{I})-F_{D}^{l}(I)\right\|_{1} \]

where \( F_{D}^{l} \) represents the feature map at discriminator network \(D\) layer \(l\).

Using a segmentation mask as input allows the generator to learn context, and requires a solution that achieves the opposite goal of AdaIN. Semantic segmentation treats multiple objects of the same class (e.g. eye segments) as a single entity ("pupil"). On the other hand, instance segmentation treats multiple objects of the same class (person-specific eye segmentation) as distinct individual objects ("pupil 1," "pupil 2"). The authors use spatially adaptive denormalization (SPADE) to allow for content injection through modulating layer activations from a generated eye image using a segmentation map input \(m\). In effect, this translates to adjusting Eqs. 3 and 4 from AdaIN to makes channel-wise adjustments, separately for each layer:

\[ \mu_{c}(x)=\frac{1}{N H W} \sum_{h=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W} x_{n c h w} \\ \sigma_{c}(x)=\sqrt{\frac{1}{N H W} \sum_{h=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W}\left(x_{n c h w}-\mu_{c}(x)\right)^{2}+\epsilon} \]

\[ \operatorname{SPADE}(x, m)=\gamma_{c h w}(m)\left(\frac{x_{nchw}-\mu(x)}{\sigma(x)}\right)+\beta_{c h w}(m) \]

where \(\mu\) and \(\sigma\) are now computed across samples (of batch size \(N\)) for the generated image, but the parameters are modulated by \(\gamma\) and $\beta$ which are learned parameters from the segmentation mask. In implementation, these values are learned through a simple 2-layer convolution network, which maps the segmentation mask to corresponding scaling and bias values at each \(h\) and \(w\) coordinate of the activation map.

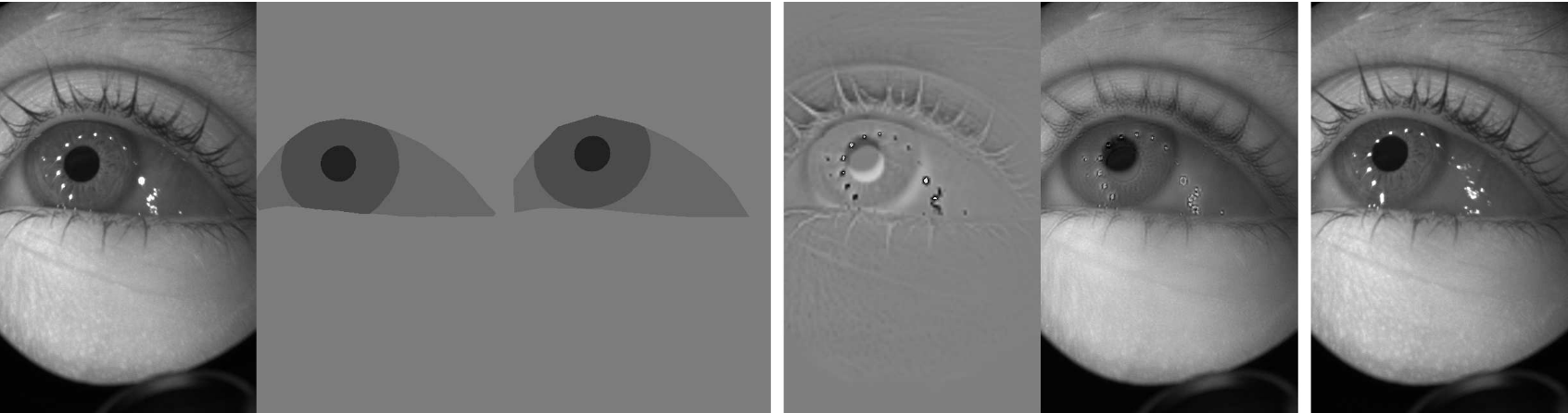
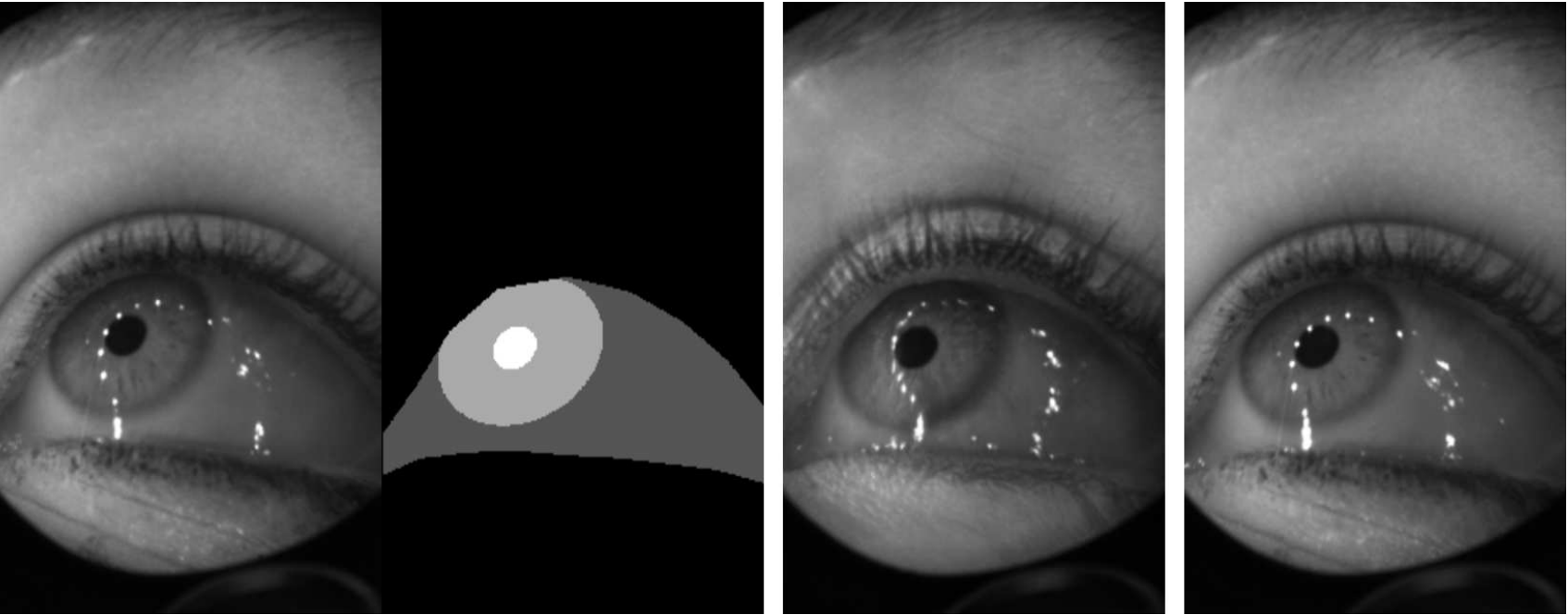
Through the use of AdaIN and Gram matrix-derived losses to control style, and SPADE and feature map-derived losses to control segmentation content, the authors applied Seg2Eye in the OpenEDS Challenge ¹¹ to generate synthetic images of eyes given a segmentation mask. The scores were computed as the L2 distance between the synthetic (\(\hat{I}\)) and ground truth (\(I\)) images associated with each mask as \(\frac{1}{H W} \sqrt{\Sigma_{i}^{H} \Sigma_{j}^{W}\left(\hat{I}_{i j}-I_{i j}\right)^{2}}\), averaged across test samples from 152 participants. While the Seg2Eye model does not match the performance level of the most accurate model, the qualitative or perceptual results (Fig. 4 in ¹²) appear much closer to the ground truth relative to the top performer (Fig. 3 in ¹³). The authors do not report the precise mean accuracy, merely that it is less than the top-performing model (\(<25.23\)).

Strengths and Limitations

One of the primary reasons why researchers often use first-order fixation measures or limited pupil response around fixations is most likely due to noise in reliably capturing eye measures. Buhler et al's computational approach appears to outperform most submissions for the OpenEDS Challenge in attempts to address this problem. The authors work has large implications to other biomedical areas of research which require high quality image data. Through modeling an individual's external eye through a segmentation map and style image references, this area of work can vastly increase ease of data collection. Provided a small reference sample, simulated viewing behavior data may be able to strengthen predictive power for attention classification tasks. However, the specificity of the authors work is hard to judge, as their image generation techniques have not been tested rigorously outside of the OpenEDS dataset. Furthermore, the authors' Seg2Eye approach is weakened by the fact that it was not the top performer, despite producing relatively better perceptually similar images to the ground truth. This indicates a mismatch between the competition assessment technique, which compares pixel-by-pixel similarity, and qualitative assessment, or human judgement, of how close the artificial images are to human eye images.